
Is floating-point math broken?
– Cato Johnston (Stack Overflow)
Formatting floating-point (FP) numbers is a surprisingly complicated task. While you can probably write a decent integer to string conversion in a matter of minutes, a good FP formatting algorithm deserves a paper in a scientific journal. One such algorithm, or rather a class of algorithms, called Grisu was published in the paper “Printing floating-point numbers quickly and accurately with integers” by Florian Loitsch in 2010. My former colleague David Gay published a technical report “Correctly rounded binary-decimal and decimal-binary conversions” in 1990. His implementation which is almost 30 years old is still widely used. A more recent development is the Ryū algorithm by Ulf Adams published in 2018 paper “Ryū: fast float-to-string conversion”.
I recently implemented a variation of the Grisu algorithm in the {fmt} formatting library and in this blog post I will describe how it works in the first approximation. The goal is to build the general intuition and I’ll leave some details for a follow-up post.
The implementation described here works with IEEE 754 double precision floating-point format which has the following bit layout (source)
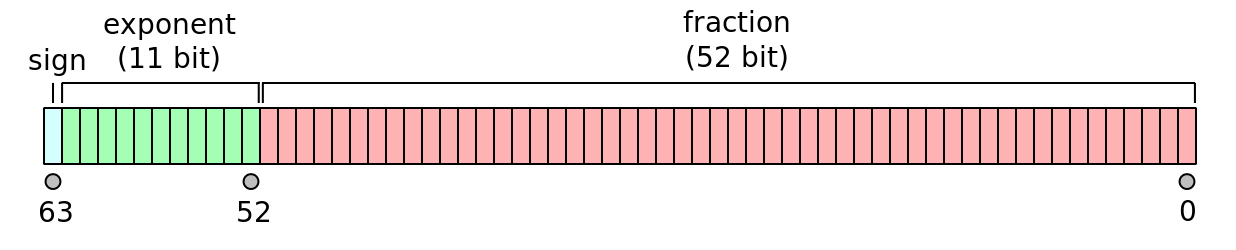
Let’s look at the π constant as an example:
#include <cmath>
#include <fmt/format.h>
int main() {
// fmt::detail::bit_cast is a portable version of std::bit_cast.
fmt::print("{:064b}\n", fmt::detail::bit_cast<uint64_t>(M_PI));
}
Output:
0100000000001001001000011111101101010100010001000010110100011000
This is not easy to parse, so let’s split the number into sign, exponent, and fraction, store them in a struct and create a simple formatter for pretty printing:
struct ieee754 {
int sign;
int biased_exponent;
uint64_t fraction;
// Significand is implicit one + the fraction (ignoring denormals, NaN, etc.)
uint64_t significand() const { return 0x10'0000'0000'0000 | fraction; }
int exponent() const { return biased_exponent - 1023; }
explicit ieee754(double value) {
auto bits = fmt::detail::bit_cast<uint64_t>(value);
sign = bits >> 63;
biased_exponent = static_cast<int>(bits >> 52) & 0x7ff;
fraction = bits & 0xf'ffff'ffff'ffff;
}
};
template <>
struct fmt::formatter<ieee754> {
auto parse(format_parse_context& ctx) { return ctx.begin(); }
auto format(ieee754 n, format_context& ctx) {
return format_to(ctx.out(), "{} {:011b} {:052b} [e = {}]",
n.sign, n.biased_exponent, n.fraction, n.exponent());
}
};
Now we can do
fmt::print("{}\n", ieee754(M_PI));
Output:
0 10000000000 1001001000011111101101010100010001000010110100011000 [e = 1]
Here 0 is a sign, 10000000000 is a biased (offset by 1023) exponent,
1001001000011111101101010100010001000010110100011000 is a fraction, and
e = 1 is the actual exponent. The value is
$$ (-1)^{\rm{sign}} 1.\rm{fraction}_2 \times 2^e = $$
$$ (-1)^0 1.1001001000011111101101010100010001000010110100011000_2 \times 2 = $$
$$ 11.001001000011111101101010100010001000010110100011000_2 $$
In this particular case converting to decimal is easy. Usual binary to decimal conversion can be applied to the integral part: $$11_2 = 3_{10}$$. The fraction can be converted by multiplying by 10, dividing by $$2^{52 - e}$$ which gives one decimal digit, then taking the remainder and repeating the operation:
// Format a fixed-point number given in the form `n * pow(2, exp)`,
// with `exp` in the range `[-63, 0]`.
std::string format_decimal(uint64_t n, int exp, int* dec_exp = nullptr) {
fmt::memory_buffer buf;
// Format the integral part:
fmt::format_int f(n >> -exp);
fmt::format_to(buf, "{}.{}", f.data()[0], f.c_str() + 1);
if (dec_exp)
*dec_exp = f.size() - 1;
// Format the fractional part:
uint64_t mask = (1ULL << -exp) - 1;
n &= mask;
for (int i = 0, num_digits = 17 - f.size(); i < num_digits; ++i) {
n *= 10;
buf.push_back('0' + (n >> -exp)); // n / pow(2, 52 - e)
n &= mask; // n % pow(2, 52 - e)
}
return fmt::to_string(buf);
}
auto pi = ieee754(M_PI);
fmt::print("{}", format_decimal(pi.significand(), pi.exponent() - 52));
Output:
3.1415926535897931
This gives 17 digits of π with the last digit a bit off due to a limited floating point precision. We can check with printf that the output is correct:
printf("%.17g\n", M_PI);
Output:
3.1415926535897931
Why 17 digits? Because for 53-bit significand (52 bit fraction + implicit 1), 17 decimal digits should be enough for the round trip, i.e. reading the number back will give the same binary representation. However, often it is possible to have much smaller number of digits and still get the correct result. For example, both 0.3 and 0.29999999999999999 are correct decimal forms of
0 01111111101 0011001100110011001100110011001100110011001100110011 [e = -2]
but you’ll probably prefer 0.3.
The “manual” conversion wasn’t hard, right? That’s because the exponent was small and we could easily fit the result of shifting by it in a 64-bit integer. The largest double has exponent of 1023 so we’d have to use arbitrary-precision arithmetic. The solution is to bring the number into a convenient exponent range by multiplying it by a suitably chosen power of 10.
Let’s look at another example, the Planck length 1.616229e−35, which has the following binary representation:
0 01110001011 0101011110111011111000000111000111010110000011100001 [e = -116]
If we multiplied it by $$ 10^{35} $$ the exponents would cancel out, and we’d be
able to use format_decimal as before. However, there are a few
problems with that: multiplication would introduce an error and it’s not clear
how to choose a suitable power of 10.
The first problem can be addressed by converting double into a handmade
floating point representation consisting of two
integers, the significand and the binary exponent. If we use a 64-bit integer
for the significand, we’ll have 11 extra bits of precision. The exponent can
easily fit into int:
struct fp {
uint64_t f;
int e;
fp(uint64_t f, int e) : f(f), e(e) {}
fp(double value) {
auto n = ieee754(value);
f = n.significand();
e = n.exponent() - 52;
}
};
template <>
struct fmt::formatter<fp> {
auto parse(format_parse_context& ctx) { return ctx.begin(); }
auto format(fp n, format_context& ctx) {
return format_to(ctx.out(), "fp({:#b}, {})", n.f, n.e);
}
};
For simplicity we don’t handle denormal numbers (that don’t have implicit one)
here, but it’s relatively straightforward to convert those to fp as well.
Let’s convert the Planck length to fp:
auto n = fp(1.616229e-35);
fmt::print("{}\n", n);
Output:
fp(0b10101011110111011111000000111000111010110000011100001, -168)
This is great but if we make use of the extra bits we should normalize the number, i.e. shift the significand left until the top-most bit is one and adjust the exponent to compensate for that:
void normalize(fp& n) {
int bits = 64 - 53;
n.f <<= bits;
n.e -= bits;
}
normalize(n);
fmt::print("{}\n", n);
Output:
fp(0b1010101111011101111100000011100011101011000001110000100000000000, -179)
To get powers of 10 for scaling, we can store a table of precomputed powers in
the normalized fp form and look them up based on the binary exponent. We don’t
need to store every representable power of 10, just enough
to bring the binary exponent into the desired range. Let’s say we don’t have
$$ 10^{35} $$ cached, but we found $$ 10^{36} $$ or, in the fp form:
fp(0b1100000010010111110011100111101111001001000001110001010110110011, 56)
Let’s multiply n by it:
auto pow10 = fp(0b1100000010010111110011100111101111001001000001110001010110110011, 56);
__uint128_t pow10_f = pow10.f, n_f = n.f;
n.f = static_cast<uint64_t>((pow10_f * n_f + (1ull << 63)) >> 64);
n.e += pow10.e + 64;
fmt::print("{}\n", n);
Output:
fp(0b1000000101001100010111101011001100010011101111100010001011011110, -59)
We add 1ull << 63 so that the result is rounded to nearest and use
__uint128_t for the computation. It’s possible to do the same portably with
just 64-bit arithmetic with a bit
more work.
The binary exponent after multiplication is -59 which means that the decimal
point is between bits 59 and 58 (zero-based):
0b10000.00101001100010111101011001100010011101111100010001011011110
and we can easily convert the result into decimal as before:
int dec_exp = 0;
auto s = format_decimal(n.f, n.e, &dec_exp);
fmt::print("{}e{:+}\n", s, dec_exp - 36);
Output:
1.6162289999999999e-35
Recall that 36 is the cached power of 10 that we found. In this case the result is not 100% correct, because it should have been rounded:
printf("%.17g\n", 1.616229e-35);
Output:
1.616229e-35
but it’s pretty close and we’ll look into rounding in the next post.
This example illustrates that the target exponent should be in the range
[-63, 0] or its subrange for convenient processing. One popular choice is
[-60, -32] where integral part fits in a 32-bit integer.
Generating cached powers of 10 can be easily done in a few lines of Python code
thanks to the built-in arbitrary precision integers, for example here’s how to
get the fp representation of $$ 10^{36} $$ used above:
binary = '{:b}'.format(10 ** 36)
f = (int('{:0<{}}'.format(binary[:65], 65), 2) + 1) / 2
e = len(binary) - 64
print('fp(0b{:064b}, {})'.format(f, e))
Output:
fp(0b1100000010010111110011100111101111001001000001110001010110110011, 56)
This is very inefficient but needs to be done only once. For the target exponent
range [-60, -32] it’s enough to generate every eighth power of 10 covering the
range of doubles.
So now we know how to approximately format floating point numbers with arbitrary exponents. However, our current implementation has a number of limitations: it always produces 17 digits of precision and it doesn’t track errors that can be introduced during computation. In the next post I’ll describe how to address these limitations and get the shortest representation.
As you might have noticed, we only used integer operations and, in particular, integer to decimal conversion. So the implementation can benefit from fast integer formatting as well as fast integer division and remainer operations such as described in the recent blog by Daniel Lemire.
Last modified on 2019-02-11